This old chestnut refuses to die and I see that it has turned up again on the BBC website. I have been intending for a while to blog about this so this has given me the excuse. I think that there has been a terrible history of misunderstanding this problem and I want to set down how the confusion comes about. People have mistaken a problem in psychology for a problem in probability.
Here is the classic statement of the problem that appeared in Parade magazine in 1990.
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?
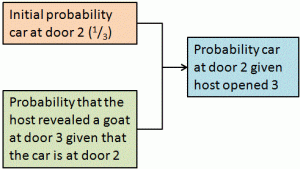
The rational way of approaching this problem is through Bayes’ theorem. Bayes’ theorem tells us how to update our views as to the probability of events when we have some new information. In this problem I have never seen anyone start from a position other than that, before any doors are opened, no door is more probably hiding the car than the others. I think it is uncontroversial to say that for each door the probability of its hiding the car is 1/3.
Once the host opens door No. 3, we have some more information. We certainly know that the car is not behind door No. 3 but does the host tell us anything else? Bayes’ theorem tells us how to ask the right question. The theorem can be illustrated like this.
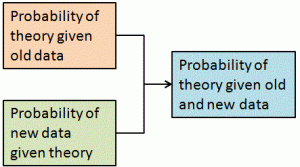
The probability of observing the new data, if the theory is correct (the green box), is called the likelihood and plays a very important role in statistics.
Without giving the details of the mathematics, Bayes’ theorem leads us to analyse the problem in this way.
We can work this out arithmetically but, because all three doors were initially equally probable, the matter comes down to deciding which of the two likelihoods is greater.
So what are the respective probabilities of the host behaving in the way he did? Unfortunately, this is where we run into problems because the answer depends on the tactic that the host was adopting.
And we are not given that in the question.
Consider some of the following possible tactics the host may have adopted.
- Open an unopened door hiding a goat, if both unopened doors have goats, choose at random.
- If the contestant chooses door 1 (or 2, or 3), always open 3 (or 1, or 2) whether or not it contains a goat.
- Open either unopened door at random but only if contestant has chosen box with prize otherwise don’t open a box (the devious strategy, suggested to me by a former girlfriend as the obviously correct answer).
- Choose an unopened door at random. If it hides a goat open it. Otherwise do not open a door (not the same as tactic 1).
- Open either unopened door at random whether or not it contains a goat
There are many more. All these various tactics lead to different likelihoods.
| Tactic | Probability that the host revealed a goat at door 3: | Rational choice | |
| given that the car is at 1 | given that the car is at 2 | ||
| 1 |
½ |
1 |
Switch |
| 2 |
1 |
1 |
No difference |
| 3 |
½ |
0 |
Don’t switch |
| 4 |
½ |
½ |
No difference |
| 5 |
½ |
½ |
No difference |
So if we were given this situation in real life we would have to work out which tactic the host was adopting. The problem is presented as though it is a straightforward maths problem but it critically hinges on a problem in psychology. What can we infer from the host’s choice? What is he up to? I think that this leads to people’s discomfort and difficulty. I am aware that even people who start out assuming Tactic 1 struggle but I suspect that somewhere in the back of their minds they cannot rid themselves of the other possibilities. The seeds of doubt have been sown in the way the problem is set.
A participant in the game show would probably have to make a snap judgment about the meaning of the new data. This is the sort of thinking that Daniel Kahneman calls System 1 thinking. It is intuitive, heuristic and terribly bad at coping with novel situations. Fear of the devious strategy may well prevail.
A more ambitious contestant may try to embark on more reflective analytical System 2 thinking about the likely tactic. That would be quite an achievement under pressure. However, anyone with the inclination may have been able to prepare himself with some pre-show analysis. There may be a record of past shows from which the host’s common tactics can be inferred. The production company’s reputation in similar shows may be known. The host may be displaying signs of discomfort or emotional stress, the “tells” relied on by poker players.
There is a lot of data potentially out there. However, that only leads us to another level of statistical, and psychological, inference about the host’s strategy, an inference that itself relies on its own uncertain likelihoods and prior probabilities. And that then leads to the level of behaviour and cognitive psychology and the uncertainties in the fundamental science of human nature. It seems as though, as philosopher Richard Jeffrey put it, “It’s probabilities all the way down”.
Behind all this, it is always useful advice that, having once taken a decision, it should only be revised if there is some genuinely new data that was surprising given our initial thinking.
Economist G L S Shackle long ago lamented that:
… we habitually and, it seems, unthinkingly assume that the problem facing … a business man, is of the same kind as those set in examinations in mathematics, where the candidate unhesitatingly (and justly) takes it for granted that he has been given enough information to construe a satisfactory solution. Where, in real life, are we justified in assuming that we possess ‘enough’ information?