Why did the polls get it wrong?

Posted on January 21, 2016 by anthonycutler

This week has seen much soul-searching by the UK polling industry over their performance leading up to the 2015 UK general election on 7 May. The polls had seemed to predict that Conservative and Labour Parties were neck and neck on the popular vote. In the actual election, the Conservatives polled 37.8% to Labour’s 31.2% leading to a working majority in the House of Commons, once the votes were divided among the seats contested. I can assure my readers that it was a shock result. Over breakfast on 7 May I told my wife that the probability of a Conservative majority in the House was nil. I hold my hands up.

An enquiry was set up by the industry led by the National Centre for Research Methods (NCRM). They presented their preliminary findings on 19 January 2016. The principal conclusion was that the failure to predict the voting share was because of biases in the way that the data were sampled and inadequate methods for correcting for those biases. I’m not so sure.

Population -> Frame -> Sample

The first thing students learn when studying statistics is the critical importance, and practical means, of specifying a sampling frame. If the sampling frame is not representative of the population of concern then simply collecting more and more data will not yield a prediction of greater accuracy. The errors associated with the specification of the frame are inherent to the sampling method. Creating a representative frame is very hard in opinion polling because of the difficulty in contacting particular individuals efficiently. It turns out that Conservative voters are harder than Labour voters to get hold of, so that they can be questioned. The NCRM study concluded that, within the commercial constraints of an opinion poll, there was a lower probability that a Conservative voter would be contacted. They therefore tended to be under-represented in the data causing a substantial bias towards Labour.

This is a well known problem in polling practice and there are demographic factors that can be used to make a statistical adjustment. Samples can be stratified. NCRM concluded that, in the run up to the 2015 election, there were important biases tending to under state the Conservative vote and the existing correction factors were inadequate. Fresh sampling strategies were needed to eradicate the bias and improve prediction. There are understandable fears that this will make polling more costly. More calls will be needed to catch Conservatives at home.

Of course, that all sounds an eminently believable narrative. These sorts of sampling frame biases are familiar but enormously troublesome for pollsters. However, I wanted to look at the data myself.

Plot data in time order

That is the starting point of all statistical analysis. Polls continued after the election, though with lesser frequency. I wanted to look at that data after the election in addition to the pre-election data. Here is a plot of poll results against time for Conservative and Labour. I have used data from 25 January to the end of 2015.^{1, 2} I have not managed to jitter the points so there is some overprinting of Conservative by Labour pre-election.

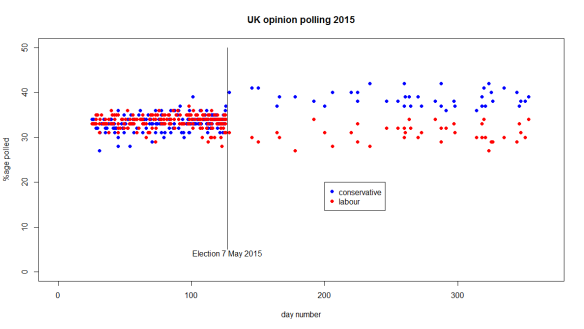
Polling201501

Now that is an arresting plot. Yet again plotting against time elucidates the cause system. Something happened on the date of the election. Before the election the polls had the two parties neck and neck. The instant (sic) the election was done there was clear red/ blue water between the parties. Applying my (very moderate) level of domain knowledge to the data before, the poll results look stable and predictable. There is a shift after the election to a new datum that remains stable and predictable. The respective arithmetic means are given below.

Party	Mean Poll Before	Election	Mean Poll After
Conservative	33.3%	37.8%	38.8%
Labour	33.5%	31.2%	30.9%

The mean of the post-election polls is doing fairly well but is markedly different from the pre-election results. Now, it is trite statistics that the variation we observe on a chart is the aggregate of variation from two sources.

Variation from the thing of interest; and
Variation from the measurement process.

As far as I can gather, the sampling methods used by the polling companies have not so far been modified. They were awaiting the NCRM report. They certainly weren’t modified in the few days following the election. The abrupt change on 7 May cannot be because of corrected sampling methods. The misleading pre-election data and the “impressive” post-election polls were derived from common sampling practices. It seems to me difficult to reconcile NCRM’s narrative to the historical data. The shift in the data certainly needs explanation within that account.

What did change on the election date was that a distant intention turned into the recall of a past action. What everyone wants to know in advance is the result of the election. Unsurprisingly, and as we generally find, it is not possible to sample the future. Pollsters, and their clients, have to be content with individuals’ perceptions of how they will vote. The vast majority of people pay very little attention to politics at all and the general level of interest outside election time is de minimis. Standing in a polling booth with a ballot paper is a very different matter from being asked about intentions some days, weeks or months hence. Most people take voting very seriously. It is not obvious that the same diligence is directed towards answering pollster’s questions.

Perhaps the problems aren’t statistical at all and are more concerned with what psychologists call affective forecasting, predicting how we will feel and behave under future circumstances. Individuals are notoriously susceptible to all sorts of biases and inconsistencies in such forecasts. It must at least be a plausible source of error that intentions are only imperfectly formed in advance and mapping into votes is not straightforward. Is it possible that after the election respondents, once again disengaged from politics, simply recalled how they had voted in May? That would explain the good alignment with actual election results.

Imperfect foresight of voting intention before the election and 20/25 hindsight after is, I think, a narrative that sits well with the data. There is no reason whatever why internal reflections in the Cartesian theatre of future voting should be an unbiased predictor of actual votes. In fact, I think it would be a surprise, and one demanding explanation, if they were so.

The NCRM report does make some limited reference to post-election re-interviews of contacts. However, this is presented in the context of a possible “late swing” rather than affective forecasting. There are no conclusions I can use.

Meta-analysis

The UK polls took a horrible beating when they signally failed to predict the result of the 1992 election in under-estimating the Conservative lead by around 8%.³ Things then felt better. The 1997 election was happier, where Labour led by 13% at the election with final polls in the range of 10 to 18%.⁴ In 2001 each poll managed to get the Conservative vote within 3% but all over-estimated the Labour vote, some pollsters by as much as 5%.⁵ In 2005, the final poll had Labour on 38% and Conservative, 33%. The popular vote was Labour 36.2% and Conservative 33.2%.⁶ In 2010 the final poll had Labour on 29% and Conservative, 36%, with a popular vote of 29.7%/36.9%.⁷ The debacle of 1992 was all but forgotten when 2015 returned to pundits’ dismay.

Given the history and given the inherent difficulties of sampling and affective forecasting, I’m not sure why we are so surprised when the polls get it wrong. Unfortunately for the election strategist they are all we have. That is a common theme with real world data. Because of its imperfections it has to be interpreted within the context of other sources of evidence rather than followed slavishly. The objective is not to be driven by data but to be led by the insights it yields.

References

Opinion polling for the 2015 United Kingdom general election. (2016, January 19). In Wikipedia, The Free Encyclopedia. Retrieved 22:57, January 20, 2016, from https://en.wikipedia.org/w/index.php?title=Opinion_polling_for_the_2015_United_Kingdom_general_election&oldid=700601063
Opinion polling for the next United Kingdom general election. (2016, January 18). In Wikipedia, The Free Encyclopedia. Retrieved 22:55, January 20, 2016, from https://en.wikipedia.org/w/index.php?title=Opinion_polling_for_the_next_United_Kingdom_general_election&oldid=700453899
Butler, D & Kavanagh, D (1992) The British General Election of 1992, Macmillan, Chapter 7
— (1997) The British General Election of 1997, Macmillan, Chapter 7
— (2002) The British General Election of 2001, Palgrave-Macmillan, Chapter 7
Kavanagh, D & Butler, D (2005) The British General Election of 2005, Palgrave-Macmillan, Chapter 7
Cowley, P & Kavanagh, D (2010) The British General Election of 2010, Palgrave-Macmillan, Chapter 7

Does noise make you fat?

Posted on June 21, 2015 by anthonycutler

“A new study has unearthed some eye-opening facts about the effects of noise pollution on obesity,” proclaimed The Huffington Post recently in another piece or poorly uncritical data journalism.

Journalistic standards notwithstanding, in Exposure to traffic noise and markers of obesity (BMJ Occupational and environmental medicine, May 2015) Andrei Pyko and eight (sic) collaborators found “evidence of a link between traffic noise and metabolic outcomes, especially central obesity.” The particular conclusion picked up by the press was that each 5 dB increase in traffic noise could add 2 mm to the waistline.

Not trusting the press I decided I wanted to have a look at this research myself. I was fortunate that the paper was available for free download for a brief period after the press release. It took some finding though. The BMJ insists that you will now have to pay. I do find that objectionable as I see that the research was funded in part by the European Union. Us European citizens have all paid once. Why should we have to pay again?

On reading …

I was though shocked reading Pyko’s paper as the Huffington Post journalists obviously hadn’t. They state “Lack of sleep causes reduced energy levels, which can then lead to a more sedentary lifestyle and make residents less willing to exercise.” Pyko’s paper says no such thing. The researchers had, in particular, conditioned on level of exercise so that effect had been taken out. It cannot stand as an explanation of the results. Pyko’s narrative concerned noise-induced stress and cortisol production, not lack of exercise.

In any event, the paper is densely written and not at all easy to analyse and understand. I have tried to pick out the points that I found most bothering but first a statistics lesson.

Prediction 101

(Almost) the first thing to learn in statistics is the relationship between population, frame and sample. We are concerned about the population. The frame is the enumerable and accessible set of things that approximate the population. The sample is a subset of the frame, selected in an economic, systematic and well characterised manner.

In Some Theory of Sampling (1950), W Edwards Deming drew a distinction between two broad types of statistical studies, enumerative and analytic.

Enumerative: Action will be taken on the frame.
Analytic: Action will be on the cause-system that produced the frame.

It is explicit in Pyko’s work that the sampling frame was metropolitan Stockholm, Sweden between the years 2002 and 2006. It was a cross-sectional study. I take it from the institutional funding that the study intended to advise policy makers as to future health interventions. Concern was beyond the population of Stockholm, or even Sweden. This was an analytic study. It aspired to draw generalised lessons about the causal mechanisms whereby traffic noise aggravated obesity so as to support future society-wide health improvement.

How representative was the frame of global urban areas stretching over future decades? I have not the knowledge to make a judgment. The issue is mentioned in the paper but, I think, with insufficient weight.

There are further issues as to the sampling from the frame. Data was taken from participants in a pre-existing study into diabetes that had itself specific criteria for recruitment. These are set out in the paper but intensify the questions of whether the sample is representative of the population of interest.

The study

The researchers chose three measures of obesity, waist circumference, waist-hip ratio and BMI. Each has been put forwards, from time to time, as a measure of health risk.

There were 5,075 individual participants in the study, a sample of 5,075 observations. The researchers performed both a linear regression simpliciter and a logistic regression. For want of time and space I am only going to comment on the former. It is the origin of the headline 2 mm per 5 dB claim.

The researchers have quoted p-values but they haven’t committed the worst of sins as they have shown the size of the effects with confidence intervals. It’s not surprising that they found so many soi-disant significant effects given the sample size.

However, there was little assistance in judging how much of the observed variation in obesity was down to traffic noise. I would have liked to see a good old fashioned analysis of variance table. I could then at least have had a go at comparing variation from the measurement process, traffic noise and other effects. I could also have calculated myself an adjusted R².

Measurement Systems Analysis

Understanding variation from the measurement process is critical to any analysis. I have looked at the World Health Organisation’s definitive 2011 report on the effects of waist circumference on health. Such Measurement Systems Analysis as there is occurs at p7. They report a “technical error” (me neither) of 1.31 cm from intrameasurer error (I’m guessing repeatability) and 1.56 cm from intermeasurer error (I’m guessing reproducibility). They remark that “Even when the same protocol is used, there may be variability within and between measurers when more than one measurement is made.” They recommend further research but I have found none. There is no way of knowing from what is published by Pyko whether the reported effects are real or flow from confounding between traffic noise and intermeasurer variation.

When it comes to waist-hip ratio I presume that there are similar issues in measuring hip circumference. When the two dimensions are divided then the individual measurement uncertainties aggregate. More problems, not addressed.

Noise data

The key predictor of obesity was supposed to be noise. The noise data used were not in situ measurements in the participants’ respective homes. The road traffic noise data were themselves predicted from a mathematical model using “terrain data, ground surface, building height, traffic data, including 24 h yearly average traffic flow, diurnal distribution and speed limits, as well as information on noise barriers”. The model output provided 5 dB contours. The authors then applied some further ad hoc treatments to the data.

The authors recognise that there is likely to be some error in the actual noise levels, not least from the granularity. However, they then seem to assume that this is simply an errors in variables situation. That would do no more than (conservatively) bias any observed effect towards zero. However, it does seem to me that there is potential for much more structured systematic effects to be introduced here and I think this should have been explored further.

Model criticism

The authors state that they carried out a residuals analysis but they give no details and there are no charts, even in the supplementary material. I would like to have had a look myself as the residuals are actually the interesting bit. Residuals analysis is essential in establishing stability.

In fact, in the current study there is so much data that I would have expected the authors to have saved some of the data for cross-validation. That would have provided some powerful material for model criticism and validation.

Given that this is an analytic study these are all very serious failings. With nine researchers on the job I would have expected some effort on these matters and some attention from whoever was the statistical referee.

Results

Separate results are presented for road, rail and air traffic noise. Again, for brevity I am looking at the headline 2 mm / 5 dB quoted for road traffic noise. Now, waist circumference is dependent on gross body size. Men are bigger than women and have larger waists. Similarly, the tall are larger-waisted than the short. Pyko’s regression does not condition on height (as a gross characterisation of body size).

BMI is a factor that attempts to allow for body size. Pyko found no significant influence on BMI from road traffic noise.

Waist-hip ration is another parameter that attempts to allow for body size. It is often now cited as a better predictor of morbidity than BMI. That of course is irrelevant to the question of whether noise makes you fat. As far as I can tell from Pyko’s published results, a 5 dB increase in road traffic noise accounted for a 0.16 increase in waist-hip ratio. Now, let us look at this broadly. Consider a woman with waist circumference 85 cm, hip 100 cm, hence waist-hip ratio, 0.85. All pretty typical for the study. Predictively the study is suggesting that a 5 dB increase in road traffic noise might unremarkably take her waist-hip ratio up over 1.0. That seems barely consistent with the results from waist circumference alone where there would not only be millimetres of growth. It is incredible physically.

I must certainly have misunderstood what the waist-hip result means but I could find no elucidation in Pyko’s paper.

Policy

Research such as this has to be aimed at advising future interventions to control traffic noise in urban environments. Broadly speaking, 5 dB is a level of noise change that is noticeable to human hearing but no more. All the same, achieving such a reduction in an urban environment is something that requires considerable economic resources. Yet, taking the research at its highest, it only delivers 2 mm on the waistline.

I had many criticisms other than those above and I do not, in any event, consider this study adequate for making any prediction about a future intervention. Nothing in it makes me feel the subject deserves further study. Or that I need to avoid noise to stay slim.

Data and anecdote revisited – the case of the lime jellybean

Posted on May 18, 2015 by anthonycutler

I have already blogged about the question of whether data is the plural of anecdote. Then I recently came across the following problem in the late Richard Jeffrey’s marvellous little book Subjective Probability: The Real Thing (2004, Cambridge) and it struck me as a useful template for thinking about data and anecdotes.

The problem looks like a staple of elementary statistics practice exercises.

You are drawing a jellybean from a bag in which you know half the beans are green, all the lime flavoured ones are green and the green ones are equally divided between lime and mint flavours.

You draw a green bean. Before you taste it, what is the probability that it is lime flavoured?

A mathematically neat answer would be 50%. But what if, asked Jeffrey, when you drew the green bean you caught a whiff of mint? Or the bean was a particular shade of green that you had come to associate with “mint”. Would your probability still be 50%?

The given proportions of beans in the bag are our data. The whiff of mint or subtle colouration is the anecdote.

What use is the anecdote?

It would certainly be open to a participant in the bean problem to maintain the 50% probability derived from the data and ignore the inferential power of the anecdote. However, the anecdote is evidence that we have and, if we choose to ignore it simply because it is difficult to deal with, then we base our assessment of risk on a more restricted picture than that actually available to us.

The difficulty with the anecdote is that it does not lead to any compelling inference in the same way as do the mathematical proportions. It is easy to see how the bean proportions would give rise to a quite extensive consensus about the probability of “lime”. There would be more variety in individual responses to the anecdote, in what weight to give the evidence and in what it tended to imply.

That illustrates the tension between data and anecdote. Data tends to consensus. If there is disagreement as to its weight and relevance then the community is likely to divide into camps rather than exhibit a spectrum of views. Anecdote does not lead to such a consensus. Individuals interpret anecdotes in diverse ways and invest them with varying degrees of credence.

Yet, the person who is best at weighing and interpreting the anecdotal evidence has the advantage over the broad community who are in agreement about what the proportion data tells them. It will often be the discipline specialist who is in the best position to interpret an anecdote.

From anecdote to data

One of the things that the “mint” anecdote might do is encourage us to start collecting future data on what we smelled when a bean was drawn. A sequence of such observations, along with the actual “lime/ mint” outcome, potentially provides a potent decision support mechanism for future draws. At this point the anecdote has been developed into data.

This may be a difficult process. The whiff of mint or subtle colouration could be difficult to articulate but recognising its significance (sic) is the beginning of operationalising and sharing.

Statistician John Tukey advocated the practice of exploratory data analysis (EDA) to identify such anecdotal evidence before settling on a premature model. As he observed:

The greatest value of a picture is when it forces us to notice what we never expected to see.

Of course, the person who was able to use the single anecdote on its own has the advantage over those who had to wait until they had compelling data. Data that they share with everybody else who has the same idea.

Data or anecdote

When I previously blogged about this I had trouble in coming to any definition that distinguished data and anecdote. Having reflected, I have a modest proposal. Data is the output of some reasonably well-defined process. Anecdote isn’t. It’s not clear how it was generated.

We are not told by what process the proportion of beans was established but I am willing to wager that it was some form of counting.

If we know the process generating evidence then we can examine its biases, non-responses, precision, stability, repeatability and reproducibility. Anecdote we cannot. It is because we can characterise the measurement process, through measurement systems analysis, that we can assess its reliability and make appropriate allowances and adjustments for its limitations. An assessment that most people will agree with most of the time. Because the most potent tools for assessing the reliability of evidence are absent in the case of anecdote, there are inherent difficulties in its interpretation and there will be a spectrum of attitudes from the community.

However, having had our interest pricked by the anecdote, we can set up a process to generate data.

Borrowing strength again

Using an anecdote as the basis for further data generation is one approach to turning anecdote into reliable knowledge. There is another way.

Today in the UK, a jury of 12 found nurse Victorino Chua, beyond reasonable doubt, guilty of poisoning 21 of his patients with insulin. Two died. There was no single compelling piece of evidence put before the jury. It was all largely circumstantial. The prosecution had sought to persuade the jury that those various items of circumstantial evidence reinforced each other and led to a compelling inference.

This is a common situation in litigation where there is no single conclusive piece of data but various pieces of circumstantial evidence that have to be put together. Where these reinforce, they inherit borrowing strength from each other.

Anecdotal evidence is not really the sort of evidence we want to have. But those who know how to use it are way ahead of those embarrassed by it.

Data is the plural of anecdote, either through repetition or through borrowing.

Unanticipated Knowledge

… Anthony Cutler's blog on operational excellence and risk management

Tag Archives: Measurement systems analysis