Tag Archives: Walter Shewhart

Shewhart chart basics 1 – The environment sufficiently stable to be predictable

Posted on by
Reply

Everybody wants to be able to predict the future. Here is the forecaster’s catechism.

  • We can do no more that attach a probability to future events.
  • Where we have data from an environment that is sufficiently stable to be predictable we can project historical patterns into the future.
  • Otherwise, prediction is largely subjective;
  • … but there are tactics that can help.
  • The Shewhart chart is the tool that helps us know whether we are working with an environment that is sufficiently stable to be predictable.

Now let’s get to work.

What does a stable/ predictable environment look like?

Every trial lawyer knows the importance of constructing a narrative out of evidence, an internally consistent and compelling arrangement of the facts that asserts itself above competing explanations. Time is central to how a narrative evolves. It is time that suggests causes and effects, motivations, barriers and enablers, states of knowledge, external influences, sensitisers and cofactors. That’s why exploration of data always starts with plotting it in time order. Always.

Let’s start off by looking at something we know to be predictable. Imagine a bucket of thousands of spherical beads. Of the beads, 80% are white and 20%, red. You are given a paddle that will hold 50 beads. Use the paddle to stir the beads then draw out 50 with the paddle. Count the red beads. Now you may, at this stage, object. Surely, this is just random and inherently unpredictable. But I want to persuade you that this is the most predictable data you have ever seen. Let’s look at some data from 20 sequential draws. In time order, of course, in Fig. 1.

Shew Chrt 1

Just to look at the data from another angle, always a good idea, I have added up how many times a particular value, 9, 10, 11, … , turns up and tallied them on the right hand side. For example, here is the tally for 12 beads in Fig. 2.

Shew Chrt 2

We get this in Fig. 3.

Shew Chrt 3

Here are the important features of the data.

  • We can’t predict what the exact value will be on any particular draw.
  • The numbers vary irregularly from draw to draw, as far as we can see.
  • We can say that draws will vary somewhere between 2 (say) and 19 (say).
  • Most of the draws are fairly near 10.
  • Draws near 2 and 19 are much rarer.

I would be happy to predict that the 21st draw will be between 2 and 19, probably not too far from 10. I have tried to capture that in Fig. 4. There are limits to variation suggested by the experience base. As predictions go, let me promise you, that is as good as it gets.

Even statistical theory would point to an outcome not so very different from that. That theoretical support adds to my confidence.

Shew Chrt 4

But there’s something else. Something profound.

A philosopher, an engineer and a statistician walk into a bar …

… and agree.

I got my last three bullet points above from just looking at the tally on the right hand side. What about the time order I was so insistent on preserving? As Daniel Kahneman put it “A random event does not … lend itself to explanation, but collections of random events do behave in a highly regular fashion.” What is this “regularity” when we can see how irregularly the draws vary? This is where time and narrative make their appearance.

If we take the draw data above, the exact same data, and “shuffle” it into a fresh order, we get this, Fig. 5.

Shew Chrt 5

Now the bullet points still apply to the new arrangement. The story, the narrative, has not changed. We still see the “irregular” variation. That is its “regularity”, that is tells the same story when we shuffle it. The picture and its inferences are the same. We cannot predict an exact value on any future draw yet it is all but sure to be between 2 and 19 and probably quite close to 10.

In 1924, British philosopher W E Johnson and US engineer Walter Shewhart, independently, realised that this was the key to describing a predicable process. It shows the same “regular irregularity”, or shall we say stable irregularity, when you shuffle it. Italian statistician Bruno de Finetti went on to derive the rigorous mathematics a few years later with his famous representation theorem. The most important theorem in the whole of statistics.

This is the exact characterisation of noise. If you shuffle it, it makes no difference to what you see or the conclusions you draw. It makes no difference to the narrative you construct (sic). Paradoxically, it is noise that is predictable.

To understand this, let’s look at some data that isn’t just noise.

Events, dear boy, events.

That was the alleged response of British Prime Minister Harold Macmillan when asked what had been the most difficult aspect of governing Britain.

Suppose our data looks like this in Fig. 6.

Shew Chrt 6

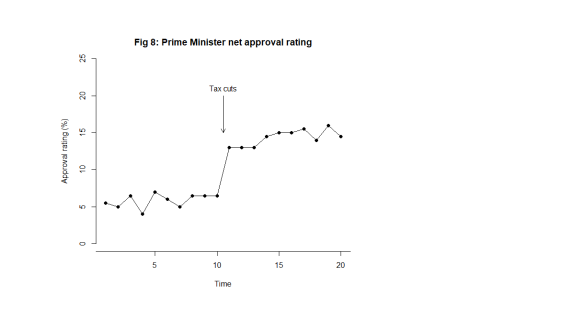
Let’s make it more interesting. Suppose we are looking at the net approval rating of a politician (Fig. 7).

Shew Chrt 7

What this looks like is noise plus a material step change between the 10th and 11th observation. Now, this is a surprise. The regularity, and the predictability, is broken. In fact, my first reaction is to ask What happened? I research political events and find at that same time there was an announcement of universal tax cuts (Fig. 8). This is just fiction of course. That then correlates with the shift in the data I observe. The shift is a signal, a flag from the data telling me that something happened, that the stable irregularity has become an unstable irregularity. I use the time context to identify possible explanations. I come up with the tentative idea about tax cuts as an explanation of the sudden increase in popularity.

The bullet points above no longer apply. The most important feature of the data now is the shift, I say, caused by the Prime Minister’s intervention.

Shew Chrt 8

What happens when I shuffle the data into a random order though (Fig. 9)?

Shew Chrt 9

Now, the signal is distorted, hard to see and impossible to localise in time. I cannot tie it to a context. The message in the data is entirely different. The information in the chart is not preserved. The shuffled data does not bear the same narrative as the time ordered data. It does not tell the same story. It does not look the same. That is how I know there is a signal. The data changes its story when shuffled. The time order is crucial.

Of course, if I repeated the tally exercise that I did on Fig. 4, the tally would look the same, just as it did in the noise case in Fig. 5.

Is data with signals predictable?

The Prime Minister will say that they predicted that their tax cuts would be popular and they probably did so. My response to that would be to ask how big an improvement they predicted. While a response in the polls may have been foreseeable, specifying its magnitude is much more difficult and unlikely to be exact.

We might say that the approval data following the announcement has returned to stability. Can we not now predict the future polls? Perhaps tentatively in the short term but we know that “events” will continue to happen. Not all these will be planned by the government. Some government initiatives, triumphs and embarrassments will not register with the public. The public has other things to be interested in. Here is some UK data.

poll20180302

You can follow regular updates here if you are interested.

Shewhart’s ingenious chart

While Johnson and de Finetti were content with theory, Shewhart, working in the manufacture of telegraphy equipment, wanted a practical tool for his colleagues that would help them answer the question of predictability. A tool that would help users decide whether they were working with an environment sufficiently stable to be predictable. Moreover, he wanted a tool that would be easy to use by people who were short of time time for analysing data and had minds occupied by the usual distractions of the work place. He didn’t want people to have to run off to a statistician whenever they were perplexed by events.

In Part 2 I shall start to discuss how to construct Shewhart’s chart. In subsequent parts, I shall show you how to use it.

#executivetimeseries

Posted on by
Reply

ExecTS1OxfordDon Wheeler coined the term executive time series. I was just leaving court in Oxford the other day when I saw this announcement on a hoarding. I immediately thought to myself “#executivetimeseries”.

Wheeler introduced the phrase in his 2000 book Understanding Variation: The Key to Managing Chaos. He meant to criticise the habitual way that statistics are presented in business and government. A comparison is made between performance at two instants in time. Grave significance is attached as to whether performance is better or worse at the second instant. Well, it was always unlikely that it would be the same.

The executive time series has the following characteristics.

  • It as applied to some statistic, metric, Key Performance Indicator (KPI) or other measure that will be perceived as important by its audience.
  • Two time instants are chosen.
  • The statistic is quoted at each of the two instants.
  • If the latter is greater than the first then an increase is inferred. A decrease is inferred from the converse.
  • Great significance is attached to the increase or decrease.

Why is this bad?

At its best it provides incomplete information devoid of context. At its worst it is subject to gross manipulation. The following problems arise.

  • Though a signal is usually suggested there is inadequate information to infer this.
  • There is seldom explanation of how the time points were chosen. It is open to manipulation.
  • Data is presented absent its context.
  • There is no basis for predicting the future.

The Oxford billboard is even worse than the usual example because it doesn’t even attempt to tell us over what period the carbon reduction is being claimed.

Signal and noise

Let’s first think about noise. As Daniel Kahneman put it “A random event does not … lend itself to explanation, but collections of random events do behave in a highly regular fashion.” Noise is a collection of random events. Some people also call it common cause variation.

Imagine a bucket of thousands of beads. Of the beads, 80% are white and 20%, red. You are given a paddle that will hold 50 beads. Use the paddle to stir the beads then draw out 50 with the paddle. Count the red beads. Repeat this, let us say once a week, until you have 20 counts. The data might look something like this.

RedBeads1

What we observe in Figure 1 is the irregular variation in the number of red beads. However, it is not totally unpredictable. In fact, it may be one of the most predictable things you have ever seen. Though we cannot forecast exactly how many red beads we will see in the coming week, it will most likely be in the rough range of 4 to 14 with rather more counts around 10 than at the extremities. The odd one below 4 or above 14 would not surprise you I think.

But nothing changed in the characteristics of the underlying process. It didn’t get better or worse. The percentage of reds in the bucket was constant. It is a stable system of trouble. And yet measured variation extended between 4 and 14 red beads. That is why an executive time series is so dangerous. It alleges change while the underlying cause-system is constant.

Figure 2 shows how an executive time series could be constructed in week 3.

RedBeads2

The number of beads has increase from 4 to 10, a 150% increase. Surely a “significant result”. And it will always be possible to find some managerial initiative between week 2 and 3 that can be invoked as the cause. “Between weeks 2 and 3 we changed the angle of inserting the paddle and it has increased the number of red beads by 150%.”

But Figure 2 is not the only executive time series that the data will support. In Figure 3 the manager can claim a 57% reduction from 14 to 6. More than the Oxford banner. Again, it will always be possible to find some factor or incident supposed to have caused the reduction. But nothing really changed.

RedBeads3

The executive can be even more ambitious. “Between week 2 and 17 we achieved a 250% increase in red beads.” Now that cannot be dismissed as a mere statistical blip.

RedBeads4

#executivetimeseries

Data has no meaning apart from its context.

Walter Shewhart

Not everyone who cites an executive time series is seeking to deceive. But many are. So anybody who relies on an executive times series, devoid of context, invites suspicion that they are manipulating the message. This is Langian statistics. par excellence. The fallacy of What you see is all there is. It is essential to treat all such claims with the utmost caution. What properly communicates the present reality of some measure is a plot against time that exposes its variation, its stability (or otherwise) and sets it in the time context of surrounding events.

We should call out the perpetrators. #executivetimeseries

Techie note

The data here is generated from a sequence of 20 Bernoulli experiments with probability of “red” equal to 0.2 and 50 independent trials in each experiment.

Productivity and how to improve it: I -The foundational narrative

Posted on by
Reply

Again, much talk in the UK media recently about weak productivity statistics. Chancellor of the Exchequer (Finance Minister) George Osborne has launched a 15 point macroeconomic strategy aimed at improving national productivity. Some of the points are aimed at incentivising investment and training. There will be few who argue against that though I shall come back to the investment issue when I come to talk about signal and noise. I have already discussed training here. In any event, the strategy is fine as far as these things go. Which is not very far.

There remains the microeconomic task for all of us of actually improving our own productivity and that of the systems we manage. That is not the job of government.

Neither can I offer any generalised system for improving productivity. It will always be industry and organisation dependent. However, I wanted to write about some of the things that you have to understand if your efforts to improve output are going to be successful and sustainable.

  • Customer value and waste.
  • The difference between signal and noise.
  • How to recognise flow and manage a constraint.

Before going on to those in future weeks I first wanted to go back and look at what has become the foundational narrative of productivity improvement, the Hawthorne experiments. They still offer some surprising insights.

The Hawthorne experiments

In 1923, the US electrical engineering industry was looking to increase the adoption of electric lighting in American factories. Uptake had been disappointing despite the claims being made for increased productivity.

[Tests in nine companies have shown that] raising the average initial illumination from about 2.3 to 11.2 foot-candles resulted in an increase in production of more than 15%, at an additional cost of only 1.9% of the payroll.

Earl A Anderson
General Electric
Electrical World (1923)

E P Hyde, director of research at GE’s National Lamp Works, lobbied government for the establishment of a Committee on Industrial Lighting (“the CIL”) to co-ordinate marketing-oriented research. Western Electric volunteered to host tests at their Hawthorne Works in Cicero, IL.

Western Electric came up with a study design that comprised a team of experienced workers assembling relays, winding their coils and inspecting them. Tests commenced in November 1924 with active support from an elite group of academic and industrial engineers including the young Vannevar Bush, who would himself go on to an eminent career in government and science policy. Thomas Edison became honorary chairman of the CIL.

It’s a tantalising historical fact that Walter Shewhart was employed at the Hawthorne Works at the time but I have never seen anything suggesting his involvement in the experiments, nor that of his mentor George G Edwards, nor protégé Joseph Juran. In later life, Juran was dismissive of the personal impact that Shewhart had had on operations there.

However, initial results showed no influence of light level on productivity at all. Productivity rose throughout the test but was wholly uncorrelated with lighting level. Theories about the impact of human factors such as supervision and motivation started to proliferate.

A further schedule of tests was programmed starting in September 1926. Now, the lighting level was to be reduced to near darkness so that the threshold of effective work could be identified. Here is the summary data (from Richard Gillespie Manufacturing Knowledge: A History of the Hawthorne Experiments, Cambridge, 1991).

Hawthorne data-1

It requires no sophisticated statistical analysis to see that the data is all noise and no signal. Much to the disappointment of the CIL, and the industry, there was no evidence that illumination made any difference at all, even down to conditions of near darkness. It’s striking that the highest lighting levels embraced the full range of variation in productivity from the lowest to the highest. What had seemed so self evidently a boon to productivity was purely incidental. It is never safe to assume that a change will be an improvement. As W Edwards Deming insisted, “In God was trust. All others bring data.”

But the data still seemed to show a relentless improvement of productivity over time. The participants were all very experienced in the task at the start of the study so there should have been no learning by doing. There seemed no other explanation than that the participants were somehow subliminally motivated by the experimental setting. Or something.

Hawthorne data-2

That subliminally motivated increase in productivity came to be known as the Hawthorne effect. Attempts to explain it led to the development of whole fields of investigation and organisational theory, by Elton Mayo and others. It really was the foundation of the management consulting industry. Gillespie (supra) gives a rich and intriguing account.

A revisionist narrative

Because of the “failure” of the experiments’ purpose there was a falling off of interest and only the above summary results were ever published. The raw data were believed destroyed. Now “you know, at least you ought to know, for I have often told you so” about Shewhart’s two rules for data presentation.

  1. Data should always be presented in such a way as to preserve the evidence in the data for all the predictions that might be made from the data.
  2. Whenever an average, range or histogram is used to summarise observations, the summary must not mislead the user into taking any action that the user would not take if the data were presented in context.

The lack of any systematic investigation of the raw data led to the development of a discipline myth that every single experimental adjustment had led forthwith to an increase in productivity.

In 2009, Steven Levitt, best known to the public as the author of Freakonomics, along with John List and their research team, miraculously discovered a microfiche of the raw study data at a “small library in Milwaukee, WI” and the remainder in Boston, MA. They went on to analyse the data from scratch (Was there Really a Hawthorne Effect at the Hawthorne Plant? An Analysis of the Original Illumination Experiments, National Bureau of Economic Research, Working Paper 15016, 2009).

LevittHawthonePlot

Figure 3 of Levitt and List’s paper (reproduced above) shows the raw productivity measurements for each of the experiments. Levitt and List show how a simple plot such as this reveals important insights into how the experiments developed. It is a plot that yields a lot of information.

Levitt and List note that, in the first phase of experiments, productivity rose then fell when experiments were suspended. They speculate as to whether there was a seasonal effect with lower summer productivity.

The second period of experiments is that between the third and fourth vertical lines in the figure. Only room 1 experienced experimental variation in this period yet Levitt and List contend that productivity increased in all three rooms, falling again at the end of experimentation.

During the final period, data was only collected from room 1 where productivity continued to rise, even beyond the end of the experiment. Looking at the data overall, Levitt and List find some evidence that productivity responded more to changes in artificial light than to natural light. The evidence that increases in productivity were associated with every single experimental adjustment is weak. To this day, there is no compelling explanation of the increases in productivity.

Lessons in productivity improvement

Deming used to talk of “disappointment in great ideas”, the propensity for things that looked so good on paper simply to fail to deliver the anticipated benefits. Nobel laureate psychologist Daniel Kahneman warns against our individual bounded rationality.

To guard against entrapment by the vanity of imagination we need measurement and data to answer the ineluctable question of whether the change we implemented so passionately resulted in improvement. To be able to answer that question demands the separation of signal from noise. That requires trenchant data criticism.

And even then, some factors may yet be beyond our current knowledge. Bounded rationality again. That is why the trick of continual improvement in productivity is to use the rigorous criticism of historical data to build collective knowledge incrementally.

If you torture the data enough, nature will always confess.

Ronald Coase

Eventually.

Deconstructing Deming VI – Institute training on the job

Posted on by
Reply

6. Institute training on the job.

W Edwards Deming Point 6 of Deming’s 14 Points. I think it was this point that made me realise that everybody projects their own anxieties onto Deming’s writings and finds what they want to find there.

Deming elaborates this point further in Out of the Crisis and several distinct positions emerge. I identify nine. In many ways, the slogan Institute training on the job is no very good description of what Deming was seeking to communicate. Not everything sits well under this heading.

“Training”, along with its sagacious uncle, “education” is one of those things that every one can be in favour of. The systems by which the accumulated knowledge of humanity are communicated, criticised and developed are the foundations of civilisation. But like all accepted truths some scrutiny repays the time and effort. Here are the nine topics I identified in Out of the Crisis.

1. People don’t spend enough on training because the benefits do not show on the balance sheet

This was one of Deming’s targets behind his sixth point. It reiterates a common theme of his. It goes back to the criticisms of Hayes and Abernathy that managers were incapable of understanding their own business. Without such understanding, a manager would lack a narrative to envision the future material rewards of current spending. Cash movements showed on the profit and loss account. The spending became merely an overhead to be attacked so as to enhance the current picture of performance projected by the accounts, the visible figures.

I have considered Hayes and Abernathy’s analysis elsewhere. Whatever the conditions of the early 1980s in the US, I think today’s global marketplace is a very different arena. Organisations vie to invest in their people, as this recent Forbes article shows (though the author can’t spell “bellwether”). True, the article confirms that development spending falls in a recession but cash flow and the availability of working capital are real constraints on a business and have to be managed. Once optimism returns, training spend takes off.

But as US satirist P J O’Rourke observed:

Getting people to give vast amounts of money when there’s no firm idea what that money will do is like throwing maidens down a well. It’s an appeal to magic. And the results are likely to be as stupid and disappointing as the results of magic usually are.

The tragedy of so many corporations is that training budgets are set and value measured on how much money is spent, in the idealistic but sentimental belief that training is an inherent good and that rewards will inevitably flow to those who have faith.

The reality is that it is only within a system of rigorous goal deployment that local training objectives can be identified so as to serve corporate strategy. Only then can training be designed to serve those objectives and only then can training’s value be measured.

2. Root Cause Analysis

The other arena in which the word “training” is guaranteed to turn up is during Root Cause Analysis. It is a moral certainty that somebody will volunteer it somewhere on the Ishikawa diagram. “To stop this happening again, let’s repeat the training.”

Yet, failure of training can never be the root cause of a problem or defect. Such an assertion yields too readily to the question Why did lack of training cause the failure?. The Why? question exposes that there was something the training was supposed to do. It could be that the root cause is readily identified and training put in place as a solution. But, the question could expose that, whatever the perceived past failures in training, the root cause, that the training would have purportedly addressed, remains obscure. Forget worrying about training until the root cause is identified within the system.

In any event, training will seldom be the best way of eliminating a problem. Redesign of the system will always be the first thing to consider.

3. Train managers and new employees

Uncontroversial but I think Deming overstated businesses’ failure to appreciate this.

4. Managers need to understand the company

Uncontroversial but I think Deming overstated businesses’ failure to appreciate this.

5. Managers need to understand variation

So much of Deming’s approach was about rigorous criticism of business data and the diligent separation of signal and noise. Those are topics that certainly have greater salience than a quarter of a century ago. Nate Silver has done much to awaken appetites for statistical thinking and the Six Sigma discipline has alerted the many to the wealth of available tools and techniques. Despite that, I am unpersuaded that genuine statistical literacy and numeracy (both are important) are any more common now than in the days of the first IBM PC.

Deming’s banner headline here is Institute training on the job. I think the point sits uncomfortably. I would have imagined that it is business schools and not employers who should apply their energies to developing and promoting quantitative skills in executives. One of the distractions that has beset industrial statistics is its propensity to create a variety of vernacular approaches with conflicting vocabularies and competing champion priorities: Taguchi methods, Six Sigma, SPC, Shainin, … . The situation is aggravated by the differential enthusiasms between corporations for the individual brands. Even within a single strand such as Six Sigma there is a frustrating variety of nomenclature, content and emphasis.

It’s not training on the job that’s needed. It is the academic industry here that is failing to provide what business needs.

6. Recognise that people learn in different ways

Of this I remain unpersuaded. I do not believe that people learn to drive motor cars in different ways. It can’t be done from theory alone. It can’t be done by writing a song about it. it comes from a subtle interaction of experience and direction. Some people learn without the direction, perhaps because they watch Nelly (see below).

Many have found a resonance between Deming’s point and the Theory of Multiple Intelligences. I fear this has distracted from some of the important themes in business education. As far as I can see, the theory has no real empirical support. Professor John White of the University of London, Institute of Education has firmly debunked the idea (Howard Gardner : the myth of Multiple Intelligences).

7. Don’t rely on watch Nelly

After my academic and vocational training as a lawyer, I followed a senior barrister around for six months, then slightly less closely for another six months. I also went to court and sat behind barristers in their first few years of practice so that I could smell what I would be doing a few months later.

It was important. So was the academic study and so was the classroom vocational training. It comes back to understanding how the training is supposed to achieve its objectives and designing learning from that standpoint.

8. Be inflexible as to work standards

This is tremendously dangerous advice for anybody lacking statistical literacy and numeracy (both).

I will come back to this but it embraces some of my earlier postings on process discipline.

9. Teach customer needs

This is the gem. Employee engagement is a popular concern. Employees who have no sight of how their job impacts the customer, who pays their wages, will soon see the process discipline that is essential to operational excellence as arbitrary and vexatious. Their mindfulness and diligence cannot but be affected by the expectation that they can operate in a cognitive vacuum.

Walter Shewhart famously observed that Data have no meaning apart from their context. By extension, continual re-orientation to the Voice of the Customer gives meaning to structure, process and procedure on the shop floor; it resolves ambiguity as to method in favour of the end-user; it fosters extrinsic, rather than intrinsic, motivation; and it sets the external standard by which conduct and alignment to the business will be judged and governed.

Ninety years on

Posted on by
Reply

Walter ShewhartOn 16 May 1924, ninety years ago today, Walter Shewhart sent his manager a short memo, no longer than one page. Shewhart described what came to be called the control chart, what we would today call a process behaviour chart.

Shewhart, a physicist by training and engineer by avocation, had been involved in improving the reliability of radio and telegraph hardware for the Western Electric Company. Equipment buried underground was often costly to repair and maintain. Shewhart had realised that the key to reliability improvement was reduction in manufactured product variation. If variation could, hypothetically, be eliminated then everything would work or everything would fail. If everything failed it would soon be fixed. Variability confounded improvement efforts.

Shewhart shared a profound insight about variation with a diverse group of independent contemporaries including Bruno de Finetti and W E Johnson. If we wanted to be able to reduce variation, we had to be able to predict it. Working to reduce variation turned on the ability to predict future behaviour.

De Finetti and Johnson were philosophers who didn’t go as far as turning their ideas into instrumental tools. The control chart turned out to be the silver bullet for predicting the future. It is a convivial tool. Shewhart invented it ninety years ago today.

If it isn’t supporting and guiding your predictions, you’re ninety years out of date (assuming that you’re reading today).

See the RearView tab at the top of the page for further background.